1. Знания и их представление

В основе систем ИИ лежат БД. Система, основанная на знаниях – система ПО, основой структуры которого является база знаний и механизмом логических выводов. В первую очередь к таким системам относят экспертные системы, способные диагностировать заболевания, оценивать месторождения полезный ископаемых, осуществлять обработку языка, текста, речи.
 Экспертная система – вычислительная система, в которую включены знания специалистов из некоторой конкретной проблемной области и которая в представлении этой области способна принимать решения.
Элементы экспертных систем:

1. база знаний
2. механизм логических выводов
3. модуль приобретения знаний
4. модуль ответов и объяснений
5. пользовательский интерфейс

1. логические модели
2. продукционные
3. сетевые модели
4. фреймовые модели

2. Логические модели

Чтобы манипулировать знаниями логического мира с помощью компьютера необходимо осуществить их моделирование. К основным методам представления знаний относят:

• логические модели
• продукционные
• сетевые модели
• фреймовые модели

в основе логической модели лежит понимание формальной системы. Все объекты, предметы, события, которые представляют собой основу общего понимания, необходимых для понимания, называются предметной областью. Предметная область включают объекты – сущности.
Сущности некоторой предметной области находятся в определённых отношениях друг с другом. Отношения между сущностями выражаются с помощью суждений. В естественном или формальном языке суждениям отвечают предложения. Языки, предназначенные для описания предметных областей называются языками представления знаний. Универсальным языком представления знаний является естественный язык. Однако его использование в системах машинного представления знаний затруднено. Причина – отсутствие формальной семантики естественного языка.
Для представления математических знаний  в математической логике используется логический формализм – исчисление высказываний и предикат. Эти формализмы имеют ясную семантику,  для них разработаны методы логического вывода, поэтому язык представлений был первым, который использовался для представления знаний каких-либо предметных областей.
Описание предметных областей, выполненное в логических языках называется логическими моделями. Логические модели, построенные с использованием языков логического программирования, используются в настоящее время для представления знаний в различных экспертных системах.

3.     Продукционные модели

В интеллектуальных системах используются различные модели представления знаний. Выбор модели зависит от предметной области, характера задачи и целей построения интеллектуальных систем. Продукционная моделей может быть использована для построения системы, которая была бы способна не только решать относительно произвольные задачи предметной области, но и демонстрировать ход решения пользователю или контролировать правильность предложенного пользователем решения.

В общем случае, система продукций представляет собой совокупность трех компонент: глобальной базы данных (ГБД), множества правил продукций и системы управления. ГБД содержит описательную информацию о предметной области. Правила продукций указывают, какие преобразования можно производить над ГБД, чтобы привести ее к некоторому терминальному виду. Система управления на каждом шаге работы выбирает, какое конкретно правило следует применить к ГБД в текущий момент времени для достижения требуемого результата. При выборе правила система управления руководствуется некоторой стратегией. Эту стратегию называют стратегией управления. Стратегия управления и правила продукций заключают в себе формализованные знания и опыт экспертов в данной предметной области.

Настоящая методика может стать основой для построения обучающей среды в формализованной предметной области. Во-первых, при наличии транслятора арифметических выражений можно контролировать ход решения, предлагаемый учеником, а, по необходимости, выявлять неверные шаги и корректировать его действия. Во-вторых, предлагаемая методика позволяет не ограничиваться заранее подготовленным набором решенных задач, а научить систему исследовать относительно произвольные ситуации. В-третьих, при возможности самостоятельного наполнения пользователем системы продукций новыми правилами она становится расширяемой до уровня, необходимого конкретному человеку в зависимости от уровня его подготовки по предмету.

В докладе рассматриваются стратегии поиска и организация оценочных функций, реализованные в машине вывода для контролирующей компоненты обучающей среды UNI_F.

4.     Сетевые модели

Достаточно часто на практике приходится сталкиваться со следующей задачей: есть таблица данных (результаты измерений, социологических опросов или обследований больных). Необходимо определить каким закономерностям подчиняются данные в таблице. Следует заметить, что характерный размер таблицы – порядка ста признаков и порядка нескольких сотен или тысяч объектов. Ручной анализ таких объемов информации фактически невозможен.
Первым шагом в решении данной задачи является группировка (кластеризация, классификация) объектов в группы (кластеры, классы) «близких» объектов. Далее исследуются вопросы того, что общего между объектами одной группы, и что отличает их от других групп. Далее будем использовать термин классификация и говорить о классах близких объектов.
Слово близких, в постановке задачи, взято в кавычки, поскольку под близостью можно понимать множество разных отношений близости. Далее будет рассмотрен ряд примеров различных видов близости.
К сожалению, вид близости и число классов приходится определять исследователю, хотя существует набор методов (методы отжига) позволяющих оптимизировать число классов.

Рассмотрим множество из m объектов , каждый из которых является n-мерным вектором с действительными координатами (в случае комплексных координат особых трудностей с данным методом также не возникает, но формулы становятся более сложными, а комплексные значения признаков случаются редко).
Зададим пространство ядер классов E, и меру близости , где a – точка из пространства ядер, а x – точка из пространства объектов. Тогда для заданного числа классов k необходимо подобрать k ядер таким образом, чтобы суммарная мера близости была минимальной. Суммарная мера близости записывается в следующем виде:

,

(1)

где  – множество объектов i-о класса.
Сеть Кохонена
Сеть Кохонена для классификации на k классов состоит из k нейронов (ядер), каждый из которых вычисляет близость объекта к своему классу. Все нейроны работают параллельно. Объект считается принадлежащим к тому классу, нейрон которого выдал минимальный сигнал. При обучении сети Кохонена считается, что целевой функционал не задан (отсюда и название «Обучение без учителя»). Однако алгоритм обучения устроен так, что в ходе обучения минимизируется функционал (1), хотя и немонотонно.

5. Фреймовые модели

В условиях бурного развития информационных технологий (ИТ) и их повсеместного внедрения дистанционного образования по-прежнему актуальными остаются вопросы создания специального программного обеспечения, поддерживающего процесс обучения. С развитием вычислительной техники на нее возлагаются все более и более серьезные задачи, в частности предпринимаются попытки использования компьютеров как средства передачи знаний. В зависимости от предметной области передача знаний может осуществляться различными способами. В случае, когда речь идет о формализованных предметных областях, усвоение знаний должно быть подкреплено умением применять их при решении различных задач.

Информационная система, способная показать пользователю процесс решения произвольной задачи гораздо более привлекательна, нежели ее аналог ориентированный на демонстрацию анализа жестко заданного набора ситуаций. Для построения подобной системы необходима специальная организация ее информационного обеспечения, а именно требуется база знаний, построенная в соответствии с определенными принципами, допускающими обработку знаний.

Предположив, что формализованные предметные области допускают построение их концептуально-логической модели в виде некоторой иерархической схемы, для реализации такой информационной структуры разумно использовать фреймовую модель представления знаний.

Идеология фреймовой модели хорошо согласуется с идеологией объектно-ориентированного программирования. Каждый объект предметной области, таким образом, может быть описан в виде некоторого класса, обладающего собственными атрибутами и методами. Наследование между классами позволяет реализовать иерархичность объектов предметной области.

В докладе рассматриваются особенности практической реализации данного подхода при создании программной оболочки, позволяющей определять объекты предметной области, их свойства и методы и преобразовывать объявленную модель предметной области в библиотеку классов, предназначенную для обработки обучающей средой UNI_F.
1. Особенности представления знаний с помощью фреймов Представление знаний с помощью фреймов явл. альтернативным по отнош. к системам продукции и лог. моделям. Оно дает возможность хранить родовидовую иерархию в явной форме.

Фрейм — составная структурная единица, предназначенная для описания относящихся к стериотипной ситуации на объекте

Осн. элемент единиц фрейма явл. слот, кот. исп. для хранения единичного знания. Станд. стр-ра слота след.:

{ имя слота; <f1> <S1>;...<fm> <Sm>; <q1> <q2>...<qn>.}

fi — имя атрибута, характерного для слота

Si — значение атрибута

qi — ссылки на другие слоты или фреймы

Стр-ра слота след-я:

имя файла

имя слота1 значение слота1

имя слота n значение слота n

Если стр-ра знаний позволяет, то при описании нужно исп-ть простые слоты, т.е. слоты, кот. имеют одно значение. Значением слота м.б. не т. константа или ссылка на др. фрейм , но и функция, кот. требует определенной детализации в процессе решения. Т. функции получили название фасет .

Фреймы-прототипы — это готов. стр-ры для описания законов опр. п/о. В них отсутствуют конкр. значения слотов. При заполнении слотов конкр. значениями, они превращаются в конкретные фреймы. Часто в системах фреймы исп-ся для стереотипных послед-й действий и тогда они наз. сушариями.

При заполнении фреймов -прототипов, часть слотов м. оставаться пустой фреймовой стр-ры дают воз-ть описывать объекты разного уровня иерархии, кот. явл. ключевым понятием.

Иерархия объектов реализуется через аппарат исследования свойств, когда классы объектов определенного уровня наследуют строения классов фреймов более высокого уровня. Если объект, кот. описывается некоторой группой фреймов находится в концептуальной связи с верхним и нижним уровнями фреймов, то соотв. ему фреймы конструируются с учетоми иерархических отношений и при этом наследование свойств осущ. через слоты или фреймы с одинаковым именем.

2. Аппарат логического вывода фреймовой модели

Логический вывод во фреймовой системе осущ. путем обмена сообщениями между фреймами разного уровня иерархии, вначале получает управление корневой фрейм, далее динам. формируется необходимая для реализации запросов цепочка фреймов след. уровня иерархии. Т.о. во фреймовой системе каждому из фреймов задается строго опр-е.

Основной операцией при работе с фреймами явл. поиск по образцу. В рамках фреймовой модели образец — это фрейм, в кот. заполнены не все стр. ед-цы, а т. те, кот. б. использованы в качестве ключа для реализации действий в конкр. фреймах.

Используются спец. процедуры наполнения слотов спец. значениями, а т. введение в систему новых фреймов-прототипов и новых связей между ними.

3. Примеры-приложения фреймовой модели

В наст. время фреймовая модель явл. основой всех объектно-ориентированных систем прог-я. В качестве наиболее популярных приложений м. назвать языки FRL,KRL, FSM, Small Talk, а также дополнения к процедурным языкам: C++, Delphi и т.д.

FRL

Реализован на базе языка LISP.

Каждый фрейм предст. собой станд. стр-ру с мах степенью вложенности <=5. Стр-ра фрейма след-я:

(имя фрейма

   (имя первого слота

               (имя первой ячейки

                           (первый коментарий)

                           (второй коментарий)...

                           (i-й коментарий))

               (имя второй ячейки

                           (...

                                       ))

   (имя второго слота

               (...

                           ))

Для указания местоположения некот. порции информации во фрейме путь

6. Понятие формальной системы

Появление формальной системы было обусловлено тем, что совершенно разные предметные области (техническая, экономическая, социальная) обладают глубоким сходством. В формальной системе, оперирующей теми или иными символами, которые воспроизводятся как элементы, с которыми обращаются согласно определённым правилам. Понятие истинности возникло  в связи с возможными интерпретациями формальной системы.
Формальные системы – это аксиоматические системы т.е. системы с наличием определённого числа заранее выбранных высказываний (аксиом). Формальная система считается заданной, если выполняются условия:

1. задано некоторое конечное или бесконечное число элементов, которое называется термами и имеется другое конечное множество, элементы которого связки или операции
2. любую линейную совокупность термов и операций называют формулой. Из множества формул выделено множество правил построения формул (ППФ), для которых задаётся правильная конструкция, которые позволяют определить, является ли формула ППФ.
3. выделено множество ППФ, называемых аксиомами ППФ формальных систем. При этом в формальной системе должна иметься процедура, определяющая, является ли ППФ аксиомой.
4. конечное множество отношений между ППФ, называемое правилами вывода.

7.     Исчисление высказываний

Пример: если студент поздно ложится спать и пьет кофе, то он утром встаёт в плохом настроении или с головной болью.
Данное предложение можно разделить на несколько простых. Если обозначить сложное высказывание через X, а остальные через Y,Z,W,P, то
X = Y и Z то W  или P
X = (Y ^ Z) → (W ?Z)
Каждую логическую связку можно рассматривать как операцию, которая образовывает новое высказывание, сложенное из более простых.

8. Исчисление предикатов первого порядка

Исчисления высказываний оказываются недостатком, например, рассуждая: всякое целое положительное число является натуральным. Число 5 – целое и положительное, следовательно, оно натуральное.
Это объясняется тем, что исчисление высказываний ограничивается структурой предложений в терминах простых высказываний. Приведённое рассуждение требует разбора подобного грамматического в смысле связи объекта и предиката.
Предикат – в грамматике – сказуемое, в логике – логическое сказуемое; это то, что в суждении высказывается как о предмете суждения.
Пусть задано некоторое множество V (V1, V2, V3…), в котором V1, V2, V3 – некоторые объекты данного множества. Обозначим любой объект из множества через Х и назовём Х предметной переменной. Тогда высказывание об этих предметах будет обозначаться P(X), где Р – предикат.
P(V1) – свойство объекта. Р(V1, V2 ) – отношение между объектами.
Высказывание о предмете может быть истинным или ложным.  Предикат на множестве V есть логическая функция, определяемая на этом множестве. При фиксировании элементов предиката получается высказывание т.е. функция превращается в высказывание.
Исчисление предикатов первого порядка представляет собой формальную систему, с помощью которой можно выразить большое разнообразие утверждений. Неотъемлемолй функцией языка предикатов является задание слов, которое описывает сущности изучаемого мира и слов , которые описывают атрибуты, их поведение и отношения.. существует 2 типа слов:

1. термы
2.  предикаты. Описание отношений.

Атомарным предикатом называется последовательность термов, заключающаяся в скобки, следующая за предметным символом. В логике предикатов атомарные предикаты задают формулы для описания отношений между сущностями.
Предложения в логике предикатов называются предикатной формулой. Отношения в логике представлены с помощью 2 классов символов:

1. отрицание, конъюнкция, дизъюнкция, импликация, эквивалентность
2. квантор общности и квантор существования.

9. Правила вывода логики предикатов

В исчислении предикатов правила построения формул (ППФ) описывают обычное предложение общего вида. Атомарный предикат является ППФ. Тогда если А и B – это ППФ , а Х – предметная переменная, то любое предложение является ППФ.
Все люди смертны: любой Х [человек(Х) → смертен(Х)]
Все аксиомы выводимы.
Если выражение (любой Х) Р(Х) является ППФ, где Х – предметная переменная, то Р(С) также является ППФ. С – значение терма.
Человек (Вася)
Человек (Коля)
Смертен(Х):- человек(Х).
? смертен(Коля).
Yes.

10. Метод резолюций

Метод резолюций основан на правиле резолюции.

Правило резолюции. Из дизъюнктов (X v F) и (¬X v G) выводим дизъюнкт (F v G). Или другими словами, дизъюнкт (F v G) является логическим следствием дизъюнктов (X v F) и (¬X v G).

Т.е. если j(X v F)=1 и j(¬X v G)=1 для некоторой интерпретации j, то j(F v G)=1. Это легко доказать. Пусть j(X v F)=1 и j(¬X v G)=1. Тогда, если j(F)=1, то и j(F v G) = 1. Если же j(F)=0, то j(X) должно быть равно 1, поскольку j(X v F)=1. Но тогда j(¬X)=0. А следовательно, j(G)=1, так как j(¬X v G)=1. Но если j(G)=1, то и j(F v G) = 1.

Введем понятие вывода. Пусть S — множество дизъюнктов. Выводом из S называется последовательность дизъюнктов D1,D2,...,Dn такая, что каждый дизъюнкт этой последовательности принадлежит S или следует из предыдущих по правилу резолюций. Дизъюнкт D выводим из S, если существует вывод из S, последним дизъюнктом которого является D.

Применение метода резолюций основано на следующем утверждении, которое называется теоремой о полноте метода резолюций.

Теорема. Множество дизъюнктов логики высказываний S невыполнимо тогда и только тогда, когда из S выводим пустой дизъюнкт.

Сам метод резолюций можно сформулировать таким образом.

Метод резолюций. Для доказательства того, что формула G является логическим следствием множества формул F1,...,Fk метод резолюций применяется следующим образом. Сначала составляется множество формул {F1,...,Fk, ¬G}. Затем каждая из этих формул приводится к конъюнктивной нормальной форме (конъюнкция дизъюнктов) и в полученных формулах зачеркиваются знаки конъюнкции. Получается множество дизъюнктов S. И, наконец, ищется вывод пустого дизъюнкта из S. Если пустой дизъюнкт выводим из S, то формула G является логическим следствием формул F1,...,Fk. Если из S нельзя вывести #, то G не является логическим следствием формул F1,...,Fk.

Рассмотрим пример доказательства методом резолюций. Пусть у нас есть следующие утверждения:
"Яблоко красное и ароматное."
"Если яблоко красное, то яблоко вкусное."
Докажем утверждение, что "яблоко вкусное".
Введем множество формул, описывающих простые высказывания, соответствующие вышеприведенным утверждениям. Пусть:
X1 — "Яблоко красное."
X2 — "Яблоко ароматное."
X3 — "Яблоко вкусное."
Тогда сами утверждения можно зависать в виде сложных формул.
X1 & X2 — "Яблоко красное и ароматное."
X1 —> X3 — "Если яблоко красное, то яблоко вкусное."
Тогда утверждение, которое надо доказать выражается формулой X3.

Итак, докажем, что X3 является логическим следствием (X1 & X2) и (X1 —> X3). Сначала составляем множество формул с отрицанием доказываемого высказывания; получаем:

{(X1 & X2), (X1 —> X3), ¬X3}.

Теперь приводим все формулы к конъюнктивной нормальной форме и зачеркиваем конъюнкции. Получаем следующее множество дизъюнктов:

{X1, X2, (¬X1 v X3), ¬X3}.

Ищем вывод пустого дизъюнкта (в этом выводе третий и последний элементы получены по правилу резолюции, остальные являются элементами исходного множества дизъюнктов):

X1, (¬X1 v X3), X3, ¬X3, #.

Получили пустой дизъюнкт, значит утверждение о том, что яблоко вкусное верно.

Метод резолюций применим и к логике предикатов первого порядка (далее просто логика первого порядка). Однако, чтобы сделать метод рабочим, требуется внести ряд изменений и дополнений в версию для логики высказываний. Мы не будем здесь вдаваться в подробности. Отметим лишь те моменты, на которые следует обратить внимание при переходе от логики высказываний к логике первого порядка.

В исчислении первого порядка мы сталкиваемся с таким понятием как переменная. Поэтому правило резолюций надо дополнить возможностью делать подстановку. Грубо говоря, подстановкой называется множество равенств между переменными и термами. Подстановка называется унификатором некоторого множества атомарных формул, если в результате подстановки все атомарные формулы множества станут одинаковыми. Если множество унифицируемо, то существует, как правило, не один унификатор этого множества, а несколько. Среди всех унификаторов данного множества выделяют, так называемый, наиболее общий унификатор. Не будем здесь определять это понятие. Здесь нам важно лишь понять, что унификатор — это подстановка, которая делает элементы некоторого множества атомарных формул одинаковыми. Отметим, что существует метод получения наиболее общего унификатора для любого множества атомарных формул.

В этой терминологии правило резолюций для логики первого порядка можно записать так.

Правило резолюции. Из дизъюнктов (P(t1,...,tn) v F) и (¬P(u1,...,un) v G) выводим дизъюнкт (s(F) v s(G)), где s — наиболее общий унификатор множества {P(t1,...,tn), P(u1,...,un)}.

Получившийся дизъюнкт (s(F) v s(G)) называют резольвентой.

11. Логическое программирование

Все существующие языки программирования основаны на некоторых общих принципах - парадигмах.
Наиболее распространенные парадигмы:

- Процедурное программирование. Память вычислительной машины условно делится на две части. В одной хранятся данные в виде переменных. В другой - команды, которые изменяют содержимое переменных. Современные процедурные языки включают различные средства структурированного программирования, что помогает упорядочить управляющие связи в программе.

Пример: Паскаль, Си.

- Объектно-ориентированное программирование (ООП). Процедуры (методы) и переменные (атрибуты) группируются в т.н. классы. ООП языки позволяют упорядочить связи по данным, т.к. доступ к переменным может выполняться явно путем вызова соответствующих методов. Сами методы чаще всего описываются в процедурном стиле.

Пример: SmallTalk, Ruby.

- Функциональное программирование (ФП). Программа рассматривается, как суперпозиция функций. Переменные отсутствуют, нет изменяемых объектов. Такой подход делает программирование ближе к математической записи задачи. Программы как правило короче и содержат меньшее кол-во ошибок, чем в императивном (процедурном) стиле.

Пример: Лисп, Хэскелл, OCAML.

- Логическое программирование (ЛП). Основано на формальной логике. Программа задается как набор логич. утверждений. Путем применения операций унификации (сопоставления) и редукции (преобразования, упрощения) система находит решение задачи. Искомые величины задаются в виде переменных в логических отношениях и запросах. (Переменная здесь не есть "переменная-ячейка памяти" в понимании процедурного программирования. В ЛП, аналогично функциональным языкам, переменная всего лишь символическое обозначение некой сущности. Значение переменной не может изменяться: оно либо найдено, либо нет. Понятие переменной в ФП и ЛП языках более точно соответствует понятию переменной в математике.)

Существуют и другие, более современные подходы в ЛП. Один из них: программирование в ограничениях. Задача формулируется как набор логических ограничений на условия. В таких языках применяется расширенное понятие переменной: недоопределенная переменная. Она имеет конкретное (возможно неизвестное на данном этапе) значение - денотат. И некую область значений, в которую денотат входит.

Пример: Пролог, Меркурий, Моцарт, CHIP.

Языки ФП и ЛП относят к программированию сверхвысокого уровня, декларативному. Т.е. в программе может не задаваться алгоритм решения в явном виде. Исходный текст ближе к естественной математической записи условий.

12.   Язык логического программирования Пролог

Главным ….. пролога является универсальный механизмом вывода, основанный на правиле резолюции.
Простейшая Пролог-программа  - это множество фактов, которое неформально называют  базой данных.
Программа состоит из фактов и правил.
Предикат – абстрактный смысл существующего отношения между термами. Предикат в прологе реализуется с помощью процедур.
Простой запрос состоит из имени предиката и стека аргументов. Наряду с термином запрос используется термин «цель».
Если в запрос входят только константы, то интерпретатор отвечает только да или нет. Ответ «да» означает, что интерпретатор смог достичь истинности запроса (достижимость поставленной цели).

Работу интерпретатора можно рассмотреть следующим образом.
Он рассматривает запрос поля как теорему, которую необходимо доказать на основе имеющихся знаний, которые записаны в виде набора фактов и правил. В вопросе содержащем переменную неявно задаётся вопрос о том, существует ли хотя бы  одно значение этой переменной, при которой достигается поставленная цель

13. Факты и правила

Программа на Прологе состоит из множества фраз, и ее можно рассматривать как сеть отношений, существующих между термами. Терм обозначает некоторую сущность, принадлежащую миру. Фраза – это либо факт, либо правило. Факт – это утверждение о том, что соблюдается некоторое конкретное отношение.
Пример:  знает (оля, витя).
Факт состоит из имени предиката знает и списка термов, заключенного в скобки.
Одним из видов термов являются атомы. Атом – это константа, которая обычно записывается в виде некоторого слова, начинающегося с маленькой буквы. Термы “оля”  и “витя” являются атомами.
Предикат может обладать произвольным количеством аргументов. Нижеследующий факт показывает, что БГТУ расположен по адресу  ул. Костюкова 48.
Простейшая Пролог-программа  - это множество фактов, которое неформально называют  базой данных.
Запросы с переменными
Переменная – это вид терма, который записывается как слово, начинающееся с большой латинской буквы, к примеру запрос:
?-знает(оля, X).
означает: “Кого знает Оля?”
В запросе, содержащем переменную, неявно спрашивается о том, существует ли хотя бы одно значение этой переменной, при котором запрос будет истинным. Приведенный запрос можно прочесть так:
“Существует ли хотя бы один человек, которого знает Оля?”
Этот запрос будет истинным, если такое лицо будет найдено в текущей базе данных “знает”.
Интерпретатор пытается согласовать аргументы запроса с аргументами фактов, входящих в базу данных “знает”.
В рассматриваемом случае запрос окажется успешным при сопоставлении запроса с первым же фактом, поскольку атом “оля” в запросе унифицируется с атомом “оля” в факте, а переменная X унифицируется с атомом “витя”, входящем в факт. В результате переменная X примет значение “витя” и интерпретатор ответит:
X = витя.
Составной запрос образуется из нескольких простых запросов, соединенных между собой символом “,” (запятая), что означает “и” или символом “;” (точка с запятой), что означает “или”. Каждый простой запрос, входящий в составной, называется “подцелью”. Истинность составного запроса зависит от истинности подцелей. Например, запрос:
?- знает(оля, A), знает(коля, A).
соответствует вопросу: “Есть ли такой человек, которого знают одновременно и Оля и Коля?”. Одна и та же переменная A входит в обе подцели этого запроса, а это означает, чо для истинности всего составного запроса вторые аргументы обеих подцелей должны принимать одно и то же значение. Интерпретатор ответит:
A = витя ,
nо
Первый ответ A = витя, показывает, что Витю одновременно знают и Оля и Коля. Второй ответ no свидетельствует, что Витя – единственный общий знакомый.
Символ подчеркивания _ выступает в качестве анонимной переменной, которая предписывает интерпретатору проигнорировать значение аргумента. Анонимная переменная унифицируется с чем угодно, но не обеспечивает выдачу выходных данных.
Правила
Правило – это факт, значение истинности которого зависит от истинных значений условий, образующих тело правила.
Форма записи правила:  заголовок :- тело.
Пример:
начальник(Familia, Oklad) :-  служ(Familia, Oklad), Oklad > 100.
Заголовок правила имеет такую же форму как и факт. Обозначение :- читается как “если”, затем следует тело правила. Каждое условие, входящее в тело, называется подцелью. Для того чтобы заголовок правила оказался истинным, необходимо, чтобы каждая подцель, входящая в тело была истинной.
Пример:

14.   Процедуры

Процедуры – множество фраз, заголовки которых совпадают и содержат одинаковое кол-во аргументов.
Смысл фразы языка Пролог может быть понят либо с позиций декларативного подхода, либо с позиций процедурного подхода. Декларативный смысл подчеркивает статическое существование отношений. Порядок следования подцелей в правиле не влияет на декларативный смысл этого правила.
При процедурной трактовке подчеркивается последовательность шагов, которые выполняет интерпретатор при обработке запроса. Таким образом приобретает значение порядок следования подцелей в правиле.
Пример: база данных “путешествие”.
Эта база данных содержит факты, каждый из которых имеет по три аргумента. Каждый факт устанавливает, что можно совершить путешествие из одного города (1-й аргумент) в другой город (2-й аргумент) воспользовавшись некоторым видом транспорта (3-й аргумент).
путешествие(белгород, орел, поезд).
путешествие(брянск, дятьково, автобус).
путешествие (губкин, белгород, автобус).
путешествие(орел, брянск, поезд).
Два правила “можно_путешествовать” устанавливают либо прямую, либо косвенную связь между двумя городами.  Косвенное отношение будет соблюдаться в том случае, если возможно путешествие из одного города в другой через третий – промежуточный город.
можно_путешествовать(A,B):- путешествие (А, B,_).                                                                           % (1)
можно_путешествовать(A,B):- путешествие(A,С,_), путешествие (С, B,_).                     % (2)
Считается, что между этими двумя правилами неявно присутствует соединитель “или”.
С декларативных позиций оба этих правила можно прочесть так:
Путешествие из города А в город B будет возможным, если либо

1. существует прямая транспортная связь между этими городами, либо
2. можно совершить путешествие из города А в некоторый промежуточный пункт С, а затем добраться из города С в город В.

Процедурная трактовка данных правил будет иной:
Для того, чтобы найти способ добраться из города А в город B, необходимо либо

1. Найти прямую трансортную связь между городами, либо
2. найти вид транспорта, связывающий город А и город C, а затем найти транспортную связь между городами С и B.

Пример запроса к базе данных можно_путешествовать:
Есть ли транспортная связь между городами Губкин и Орел?
?- можно_путешествовать(губкин, орел).
Yes 
Ответ получен по фразе (2).
При обработке этого запроса интерпретатор вначале проверяет фразу (1). Если фраза (1) дает отрицательный ответ, то интерпретатор переходит к проверке фразы (2).
Обработку последнего запроса можно представить в виде эквивалентной последовательности запросов:
?-можно_путешествовать(губкин, орел).
              
                   %первая подцель первого правила “можно_путешествовать”
                   ?- путешествие (губкин, орел,_).
                   no
                   %первая подцель второго правила “можно_путешествовать”
                   ?- путешествие (губкин, С,_).
                   С = белгород
                   %вторая подцель второго правила “можно_путешествовать”
                   ?- путешествие (белгород, орел,_).
                   yes
yes

15. Рекурсивные процедуры

Классическим примером рекурсивного определения в Прологе может служить программа «предок».
Предположим, имеем  дерево родственных отношений:

Создадим соответствующую базу данных  “родитель”
родитель(пам,боб).
родитель(том,боб).
родитель(том,лиз).
родитель(боб,энн).
родитель(боб,пат).
родитель( пат, джим).

Создадим также два правила:
предок(A,B):- родитель(A,B).                                                  %(1)
предок(A,B):- родитель(С,B), предок(A, C).                          %(2)

Первое правило – для ближайших предков.  Второе  для отдаленных предков.

Любая рекурсивная процедура должна включать по крайней мере по одной из компонент:

1. Нерекурсивную фразу, определяющую исходный вид процедуры, т.е. вид процедуры в момент прекращения рекурсии.
2. Рекурсивное правило. Первая подцель, располагающаяся в теле этого правила, вырабатывает новые значения аргументов. Далее размещается рекурсивная подцель, в которой используются новые значения аргументов.

Фраза (1) процедуры предок определяет исходный вид этой процедуры. Как только данная фраза станет истинной, дальнейшая рекурсия прекратится. Фраза (2) – это рекурсивное правило. При каждом вызове данное правило поднимается на одно поколение вверх. Подцель родитель(С, B), входящая в тело этого правила, вырабатывает значение переменной С. Затем располагается рекурсивная подцель предок(A, C), в которой используется этот новый аргумент.

16. Типы отношений

Логические отношения/Зависимости (Logical Relationship) — зависимость между двумя работами проекта или между работой проекта и ключевым событием. См. также Отношения предшествования. Используются, как правило, четыре типа логических отношений (взаимосвязей между граничными точками двух работ):

«Окончание-Начало»: предшествующая работа должна закончиться до того, как последующая работа может начаться.

«Окончание-Окончание»: предшествующая работа должна закончиться до того, как закончится последующая работа.

«Начало-Начало»: предшествующая работа должна начаться до того, как последующая работа может начаться.

«Начало-Окончание»: предшествующая работа должна начаться до того, как последующая работа может закончиться.
В ОСМ используются также зависимости между произвольными точками двух работ.

17. Механизм ответов Пролог-системы на вопросы

Вопрос к системе - это всегда последовательность, состоящая из одной или нескольких целей. Для того, чтобы ответить на вопрос, система пытается достичь всех целей. Что значит достичь цели? Достичь цели - это значит показать, что утверждения, содержащиеся в вопросе, истинны в предположении, что все отношения программы истинны. Другими словами, достичь цели - это значит показать, что она логически следует из фактов и правил программы. Если вопрос содержит переменные, система должна к тому же найти конкретные объекты, которые (будучи подставленными вместо переменных) обеспечивают достижение цели. Найденные конкретизации сообщаются пользователю. Если для некоторой конкретизации система не в состоянии вывести цель из остальных предложений программы, то ее ответом на вопрос будет "нет".Таким образом, подходящей интерпретацией пролог-программы в математических терминах будет следующая: пролог-система рассматривает факты и правила в качестве множества аксиом, а вопрос пользователя - как теорему; затем она пытается доказать эту теорему, т.е. показать, что ее можно логически вывести из аксиом. Проиллюстрируем этот подход на классическом примере. Пусть имеются следующие аксиомы:                                 Все люди смертны.
        Сократ - человек.
Теорема, логически вытекающая из этих двух аксиом:
        Сократ смертен.
Первую из вышеуказанных аксиом можно переписать так:
        Для всех X, если X - человек, то X смертен.
Соответственно наш пример можно перевести на Пролог следующим образом:
       смертен( X) :- человек( X).                    % Все люди смертны
       человек( сократ).                                     % Сократ - человек
       ?-  смертен( сократ).                                % Сократ смертен?
       yes                   (да)
Более сложный пример из программы о родственных отношениях, приведенной на рис. 1.8:
       ?-  предок( том, пат)
Мы знаем, что родитель( боб, пат) - это факт. Используя этот факт и правило пр1, мы можем сделать вывод, что утверждение предок( боб, пат) истинно. Этот факт получен в результате вывода - его нельзя найти непосредственно в программе, но можно вывести, пользуясь содержащимися в ней фактами и правилами. Подобный шаг вывода можно коротко записать
       родитель( боб, пат) ==> предок( боб, пат)
Эту запись можно прочитать так: из родитель( боб, пат) следует предок( боб, пат) на основании правила пр1. Далее, нам известен факт родитель( том, боб). На основании этого факта и выведенного факта предок( боб, пат) можно заключить, что, в силу правила пр2, наше целевое утверждение предок( том, пат) истинно. Весь процесс вывода, состоящий из двух шагов, можно записать так:
       родитель(боб, пат) ==> предок( боб, пат)
        родитель(том, боб)  и   предок( боб, пат)    ==>
               предок( том, пат)
Таким образом, мы показали, какой может быть последовательность шагов для достижения цели, т.е. для демонстрации истинности целевого утверждения. Назовем такую последовательность цепочкой доказательства. Однако мы еще не показали как пролог-система в действительности строит такую цепочку.
Пролог-система строит цепочку доказательства в порядке, обратном по отношению к тому, которым мы только что воспользовались. Вместо того, чтобы начинать с простых фактов, приведенных в программе, система начинает с целей и, применяя правила, подменяет текущие цели новыми, до тех пор, пока эти новые цели не окажутся простыми фактами. Если задан вопрос
       ?-  предок( том, пат).
система попытается достичь этой цели. Для того, чтобы это сделать, она пробует найти такое предложение в программе, из которого немедленно следует упомянутая цель. Очевидно, единственными подходящими для этого предложениями являются пр1 и пр2.

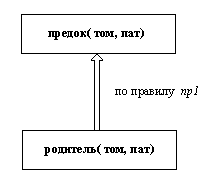
Рис. 1. 9.  Первый шаг вычислений. Верхняя цель истинна, если истинна нижняя.
Это правила, входящие в отношение предок. Будем говорить, что головы этих правил сопоставимы с целью.
Два предложения пр1 и пр2 описывают два варианта продолжения рассуждений для пролог-системы. Вначале система пробует предложение, стоящее в программе первым:
       предок( X, Z) :- родитель( X, Z).
Поскольку цель - предок( том, пат), значения переменным должны быть приписаны следующим образом:
       X  =  том,  Z  =   пат
Тогда исходная цель предок( том, пат) заменяется новой целью:
       родитель( том, пат)
Такое действие по замене одной цели на другую на основании некоторого правила показано на рис. 1.9. В программе нет правила, голова которого была бы сопоставима с целью родитель(том, пат), поэтому такая цель оказывается неуспешной. Теперь система делает возврат к исходной цели, чтобы попробовать второй вариант вывода цели верхнего уровня предок( том, пат). То есть, пробуется правило пр2:
       предок( X, Z) :-
               родитель( X, Y),
               предок( Y, Z).
Как и раньше, переменным X и Z приписываются значения:
       X  =  том,   Z   =  пат
В этот момент переменной Y еще не приписано никакого значения. Верхняя цель предок( том, пат) заменяется двумя целями:
       родитель( том, Y),
        предок( Y, пат)
Этот шаг вычислений показан на рис. 1.10, который представляет развитие ситуации, изображенной на рис. 1.9.

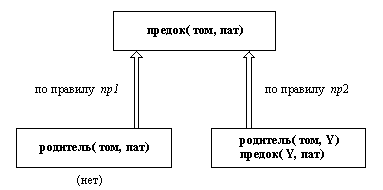
Рис. 1. 10.  Продолжение процесса вычислений, показанного на рис. 1.9.
Имея теперь перед собой две цели, система пытается достичь их в том порядке, каком они записаны. Достичь первой из них легко, поскольку она соответствует факту из программы. Процесс установления соответствия - сопоставление (унификация) вызывает приписывание переменной Y значения боб. Тем самым достигается первая цель, а оставшаяся превращается в
       предок( боб, пат)
Для достижения этой цели вновь применяется правило пр1. Заметим, - что это (второе) применение правила никак не связано с его первым применением. Поэтому система использует новое множество переменных правила всякий раз, как оно применяется. Чтобы указать это, мы переименуем переменные правила пр1 для нового его применения следующим образом:
       предок( X ', Z ') :-
               родитель( X ', Z ').
Голова этого правила должна соответствовать нашей текущей цели предок( боб, пат). Поэтому
       X '  =  боб,   Z '   =  пат
Текущая цель заменяется на
       родитель( боб, пат)
Такая цель немедленно достигается, поскольку встречается в программе в качестве факта. Этот шаг завершает вычисление, что графически показано на рис. 1.11.

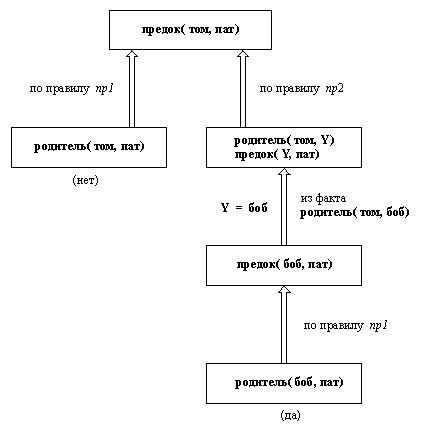
Рис. 1. 11.  Все шаги достижения цели предок( том, пат). Правая
ветвь демонстрирует, что цель достижима.
Графическое представление шагов вычисления на рис. 1.11 имеет форму дерева. Вершины дерева соответствуют целям или спискам целей, которые требуется достичь. Дуги между вершинами соответствуют применению (альтернативных) предложений программы, которые преобразуют цель, соответствующую одной вершине, в цель, соответствующую другой вершине. Корневая (верхняя) цель достигается тогда, когда находится путь от корня дерева (верхней вершины) к его листу, помеченному меткой "да". Лист помечается меткой "да", если он представляет собой простой факт. Выполнение пролог-программы состоит в поиске таких путей. В процессе такого поиска система может входить и в ветви, приводящие к неуспеху. В тот момент, когда она обнаруживает, что ветвь не приводит к успеху, происходит автоматический возврат к предыдущей вершине, и далее следует попытка применить к ней альтернативное предложение.

18. Декларативный и процедурный смысл пролог-программ

До сих пор во всех наших примерах всегда можно было понять результаты работы программы, точно не зная, как система в действительности их нашла. Поэтому стоит различать два уровня смысла программы на Прологе, а именно:

• декларативный смысл и
• процедурный смысл .

Декларативный смысл касается только отношений, определенных в программе. Таким образом, декларативный смысл определяет, что должно быть результатом работы программы. С другой стороны, процедурный смысл определяет еще и как этот результат был получен, т. е. как отношения реально обрабатываются пролог-системой.
Способность пролог-системы прорабатывать многие процедурные детали самостоятельно считается одним из специфических преимуществ Пролога. Это свойство побуждает программиста рассматривать декларативный смысл программы относительно независимо от ее процедурного смысла. Поскольку результаты работы программы в принципе определяются ее декларативным смыслом, последнего (Опять же в принципе) достаточно для написания программ. Этот факт имеет практическое значение, поскольку декларативные аспекты программы являются, обычно, более легкими для понимания, нежели процедурные детали. Чтобы извлечь из этого обстоятельства наибольшую пользу, программисту следует сосредоточиться главным образом на декларативном смысле и по возможности не отвлекаться на детали процесса вычислений. Последние следует в возможно большей мере предоставить самой пролог-системе.
Такой декларативный подход и в самом деле часто делает программирование на Прологе более легким, чем на таких типичных процедурно-ориентированных языках, как Паскаль. К сожалению, однако, декларативного подхода не всегда оказывается, достаточно. Далее станет ясно, что, особенно в больших программах, программист не может полностью игнорировать процедурные аспекты по соображениям эффективности вычислений. Тем не менее следует поощрять декларативный стиль мышления при написании пролог-программ, а процедурные аспекты игнорировать в тех пределах, которые устанавливаются практическими ограничениями.

Резюме

• Программирование на Прологе состоит в определении отношений и в постановке вопросов, касающихся этих отношений.
• Программа состоит из предложений. Предложения бывают трех типов: факты, правила и вопросы.
• Отношение может определяться фактами, перечисляющими n-ки объектов, для которых это отношение выполняется, или же оно может определяться правилами.
• Процедура - это множество предложений об одном и том же отношении.
• Вопросы напоминают запросы к некоторой базе данных. Ответ системы на вопрос представляет собой множество объектов, которые удовлетворяют запросу.
• Процесс, в результате которого пролог-система устанавливает, удовлетворяет ли объект запросу, часто довольно сложен и включает в себя логический вывод, исследование различных вариантов и, возможно, возвраты. Все это делается автоматически самой пролог-системой и по большей части скрыто от пользователя.
• Различают два типа смысла пролог-программ: декларативный и процедурный. Декларативный подход предпочтительнее с точки зрения программирования. Тем не менее, программист должен часто учитывать также и процедурные детали.
• В данной главе были введены следующие понятия:
  
      предложение, факт, правило, вопрос
      голова предложения, тело предложения
      рекурсивное правило
      рекурсивное определение
      процедура
      атом, переменная
      конкретизация переменной
      цель
      цель достижима, цель успешна
      цель недостижима,
      цель имеет неуспех, цель терпит неудачу
      возврат
      декларативный смысл, процедурный смысл.

19. Объекты данных Пролога

На рис. 2.1 приведена классификация объектов данных Пролога. Пролог-система распознает тип объекта по его синтаксической форме в тексте программы. Это возможно благодаря тому, что синтаксис Пролога

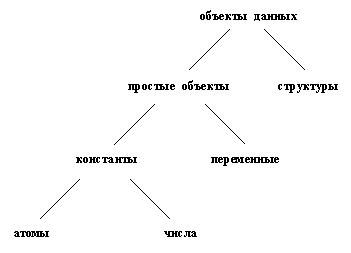
Рис. 2. 1.  Обьекты данных Пролога.
предписывает различные формы записи для различных типов объектов данных. В гл. 1 мы уже видели способ, с помощью которого можно отличить атомы от переменных: переменные начинаются с прописной буквы, тогда как атомы - со строчной. Для того, чтобы пролог-система распознала тип объекта, ей не требуется сообщать больше никакой дополнительной информации (такой, например, как объявление типа данных).

20. Списки

Список - это простая структура данных, широко используемая в нечисловом программировании. Список - это последовательность, составленная из произвольного числа элементов, например энн, теннис, том, лыжи. На Прологе это записывается так:
        [ энн, теннис, том, лыжи ]
Однако таково лишь внешнее представление списков. Как мы уже видели в гл. 2, все структурные объекты Пролога - это деревья. Списки не являются исключением из этого правила.
Каким образом можно представить список в виде стандартного прологовского объекта? Мы должны рассмотреть два случая: пустой список и не пустой список. В первом случае список записывается как атом  [ ].  Во втором случае список следует рассматривать как структуру состоящую из двух частей:
(1)    первый элемент, называемый головой списка;
(2)    остальная часть списка, называемая хвостом.
Например, для списка
        [ энн, теннис, том, лыжи ]
энн - это голова, а хвостом является список
        [ теннис, том, лыжи ]
В общем случае, головой может быть что угодно (любой прологовский объект, например, дерево или переменная); хвост же должен быть списком. Голова соединяется с хвостом при помощи специального функтора. Выбор этого функтора зависит от конкретной реализации Пролога; мы будем считать, что это точка:
        .( Голова, Хвост)
Поскольку Хвост - это список, он либо пуст, либо имеет свои собственную голову и хвост. Таким образом, выбранного способа представления списков достаточно для представления списков любой длины. Наш список представляется следующим образом:
        .( энн, .( теннис, .( том, .( лыжи, [ ] ) ) ) )
На рис. 3.1 изображена соответствующая древовидная структура. Заметим, что показанный выше пример содержит пустой список [ ]. Дело в том, что самый последний хвост является одноэлементным списком:
        [ лыжи ]
Хвост этого списка пуст
        [ лыжи ] = .( лыжи, [ ] )
Рассмотренный пример показывает, как общий принцип структуризации объектов данных можно применить к спискам любой длины. Из нашего примера также видно, что такой примитивный способ представления в случае большой глубины вложенности подэлементов в хвостовой части списка может привести к довольно запутанным выражениям. Вот почему в Прологе предусматривается более лаконичный способ изображения списков, при котором они записываются как последовательности элементов, заключенные в квадратные скобки. Программист может использовать оба способа, но представление с квадратными скобками, конечно, в большинстве случаев пользуется предпочтением. Мы, однако, всегда будем помнить, что это всего лишь косметическое улучшение и что во внутреннем представлении наши списки выглядят как деревья. При выводе же они автоматически преобразуются в более лаконичную форму представления. Так, например, возможен следующий диалог:
        ?-  Список1 = [а, b, с],
             Список2 = (a,  .(b,  .(c,[ ]) ) ).
        Список1 = [а, b, с]
        Список2 = [а, b, с]
        ?-  Увлечения1 = .( теннис, .(музыка, [ ] ) ),
             Увлечения2 = [лыжи, еда],
             L = [энн, Увлечения1, том, Увлечения2].
        Увлечения1 = [теннис, музыка]
        Увлечения2 = [лыжи, еда]
        L = [энн, [теннис, музыка], том, [лыжи, еда]]

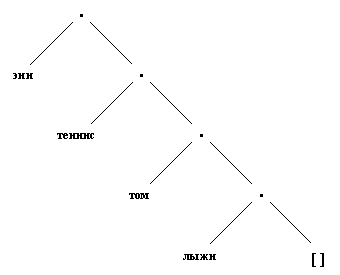
Рис. 3. 1.  Представление списка [энн, теннис, том, лыжи] в виде дерева.
Приведенный пример также напоминает вам о том, что элементами списка могут быть любые объекты, в частности тоже списки.
На практике часто бывает удобным трактовать хвост списка как самостоятельный объект. Например, пусть
        L = [а, b, с]
Тогда можно написать:
        Хвост = [b, с] и L = .(а, Хвост)
Для того, чтобы выразить это при помощи квадратных скобок, в Прологе предусмотрено еще одно расширение нотации для представления списка, а именно вертикальная черта, отделяющая голову от хвоста:
        L = [а | Хвост]
На самом деле вертикальная черта имеет более общий смысл: мы можем перечислить любое количество элементов списка, затем поставить символ " | ", а после этого - список остальных элементов. Так, только что рассмотренный пример можно представить следующими различными способами:
        [а, b, с] = [а | [b, с]] = [a, b | [c]] = [a, b, c | [ ]]
Подытожим:

• Список - это структура данных, которая либо пуста, либо состоит из двух частей: головы и хвоста. Хвост в свою очередь сам является списком.
• Список рассматривается в Прологе как специальный частный случай двоичного дерева. Для повышения наглядности программ в Прологе предусматриваются специальные средства для списковой нотации, позволяющие представлять списки в виде
  
          [ Элемент1, Элемент2, ... ]
  
  или
  
          [ Голова | Хвост ]
  
  или
  
          [ Элемент1, Элемент2, ... | Остальные]

21. Управление выполнением программы на Прологе

Работу интерпретатора языка Пролог можно трактовать как рекурсивный циклический процесс унификации и вычисления подцелей. Действия интерпретатора инициируются запросом. В ходе выполнения этих действий интерпретатор «опустится» в структуру текущей программы настолько глубоко, насколько это окажется необходимым для того, чтобы найти факты, требующиеся для определения истинностного значения запроса. Затем интерпретатор вернется в исходное состояние, доказав или оказавшись не в состоянии доказать истинность запроса.
После того как пользователь вводит запрос интерпретатору, этот запрос активизируется. Интерпретатор приступает к анализу фраз текущей программы в поисках первой фразы, заголовок которой будет унифицироваться с запросом.
Указание интерпретатору вернуться назад.
После того как интерпретатор найдет один ответ на запрос, пользователь может попросить найти еще один ответ. Для этого вводится символ ; , который означает отказ от только что полученного ответа. Это заставляет интерпретатор возвратиться назад и приступить к поиску другого ответа. Точнее, ввод символа ; приводит к неудаче запроса, активизированного самым последним (т.е.  запроса, расположенного в вершине стека).
Предикат «Сократить»
Пространство поиска запроса – это множество всех возможных ответов, рассматриваемых интерпретатором при выполнении запроса. Существует специальный встроенный предикат «сократить», который дает указание интерпретатору не возвращаться назад далее той точки, где стоит этот предикат.
Пример запроса с предикатом «сократить»:
?- a(X), b(Y), !, с(X,Y,Z).
При выполнении данного запроса интерпретатор пройдет через предикат «сократить» только в том случае, если подцель а(X) и b(X) окажутся успешными. После того как предикат «сократить» будет обработан интерпретатор не сможет возвратиться назад для повторного рассмотрения подцелей «a» и «b», если подцель «с» потерпит неудачу при текущих значениях переменных X и Y.
Проверка типа терма
В языке Пролог имеются встроенные предикаты, предназначенные для проверки типа терма.
var(X)
Этот предикат даст значение истина, если его аргумент будет не конкретизированной переменной. Пример:
?- var(X)
да
?- X = лондон, var(X).
нет

nonvar(X)
Этот предикат будет истинным, если его аргумент будет термом любого вида, кроме не конкретизированной переменной. Пример:
?- X = [париж, лондон, нью-йорк, токио],  nonvar(X).
да

Действия с текущей программой

Существуют встроенные предикаты, позволяющие программными средствами изменять текущее множество фраз программы.
Предикат assert (принять) добавляет к текущей программе фразу X.
Предикат retract (удалить) удаляет из текущей программы первую фразу, которая унифицируется с X.

22. Динамические базы данных

В каждый момент выполнения пролог-программы лишь два файла являются "активными": один для ввода, другой - для вывода. Эти два файла называются текущим входным потоком и текущим выходным потоком соответственно. В начальный момент эти два потока соответствуют терминалу. Текущий входной поток может быть заменен на другой файл ИмяФайла посредством цели

        see( ИмяФайла)                                     ( Смотри(ИмяФайла) )

Такая цель всегда успешна (если только с файлом ИмяФайла все в порядке), а в качестве побочного эффекта происходит переключение ввода с предыдущего входного потока на файл ИмяФайла. Поэтому типичным примером использования предиката see является следующая последовательность целей, которая считывает информацию из файла файл1, а затем переключается обратно на терминал:

        . . .
        see( файл1),
        читать_из_файла( Информация),
        see( user)

Текущий выходной поток может быть изменен при помощи цели вида

        tell( ИмяФайла)                       ( сообщить( ИмяФайла) )

Следующая последовательность целей выводит некоторую информацию в файл3, а после этого перенаправляет последующий вывод обратно на терминал:

. . .
        tell( файл3),
        записать_в_файл( Информация),
        tell( user),
        . . .        

        Цель

        seen                                          ( конец чтения)

закрывает текущий входной файл. Цель

        told                                           ( конец записи)

закрывает текущий выходной файл.

Существуют два основных способа, с помощью которых файлы рассматриваются в Прологе в зависимости от формы записанной в них информации. Один способ - рассматривать символ как основной элемент файла. Соответственно один запрос на ввод или вывод приведет к чтению или записи одного символа. Для этой цели предназначены встроенные предикаты get, get0 и put (получить, получить0 и выдать).

Другой способ рассматривать файл - считать, что в качестве основных элементов построения файла используются более крупные единицы текста. Такой естественной более крупной единицей является прологовский терм. Поэтому каждый запрос на ввод/вывод такого типа приведет к переносу целого терма из текущего входного потока или в текущий выходной поток соответственно. Предикатами для переноса термов являются предикаты read и write (читать и писать). В этом случае информация в файле должна, конечно, по форме соответствовать синтаксису термов.

Существуют встроенные предикаты, позволяющие программными средствами изменять текущее множество фраз программы.
Предикат assert (принять) добавляет к текущей программе фразу X.

Предикат retract (удалить) удаляет из текущей программы первую фразу, которая унифицируется с X.

23. Представление знаний фреймами в Прологе

Каждый фрейм содержит слоты, которые идентифицируют тип ситуации или задают параметры ситуации.
Пример: фрейм, описывающий ситуацию на предприятии.
Слоты:
                Тип
                Время, место.
Формализм фрейма м. рассматриваться как обобщение формализма семантических сетей.

1. Иерархия – одна из важнейших концепций формализма фреймов. М. использоваться для описания топологии знаний.
2. Наследование – м. дать указание, что если значение одного из слотов в фрейме не задано, то фрейм должен получить значение по умолчанию фрейма более высокого уровня.

Пример:
разновидность(собрание, мероприятие).
разновидность(собрание_38,собрание).

Значение слотов для фрейма собрание:
-время,
-место.
                собрание(время, “Среда 14:00”).
      собрание(место, “Зал заседаний”).
      собрание_38(присутствующие, [Коля, Вася, Саша]).
Правила наследования:
                собрание_38 (атрибут, значение):-разновидность(собрание_38,собрание),
            Подцель=…[Фрейм,Атрибут,Значение],Подцель.
После этого производится преобразование списка в факт, и получается фрейм (Атрибут, Значение).

собрание_38(время,X).
X = среда 14:00.  %это по умолчанию

собрание_38(время,”четверг 9:00”).

Отношение между Собрание_38 и временем его проведения должно относиться 1 к 1. Эта проблема решается с пом. предиката Сократить(!).
               

Заменим предложение:
разновидность(Собрание,Мероприятие).
      Разновидность(С_38,собрание).
Собрание_38(Атрибут,Значение):-С_38(Атрибут,Значение),!.
Собрание_38(Атрибут,Значение):-разновидность(С_38,Фрейм),
      Подцель=...[Фрейм,Атрибут,Значение],Подцель.

С_38(Присутствуют,[Коля,Маша,Миша]).
С_38(Время, “Четверг 9:00”).

Собрание_38(Время,X).

24. Реализация на прологе семантических сетей

В семантических сетях сущности и классы сущностей ассоциируются с узлами, отношения ассоциируются с дугами, соединяющими узлы.
Дуга, присоединенная к одному узлу, определяет свойства узла.
Семантическая сеть позволяет осуществить вывод по цепочкам, описываемых определенными видами дуг.

Пример:

Важнейшей концепцией семантических сетей является иерархия.
Формализм сем. сетей является удобным средством для представления таксономии знаний. Каждый уровень таксономии является узлом, соединяемым с другим отношением «является».
Птица – высший уровень таксономии. На сл. могут располагаться виды птиц. Ниже – конкретный представитель.
Пример семантической модели
                является(канарейка, птица).
      является(аня,канарейка).
      летает(птица).
      цвет(канарейка,желтый).

      цвет(X,Y):-является(X,Z),цвет(Z,Y).
      летает(X):-является(X,Y),летает(Y).

25. Объектно-ориентированное программирование на Прологе

Механизм наследования – метод представления многих состояний знаний, при котором конкретное состояние может наследовать информацию от общего.
Фраза становится в соответствие состоянию путем добавления в заголовок фразы в виде первого ее аргумента.
                время(Собрание, «Среда 14:00»).
время(собрание_38, «Четверг 9:00»).
Отношение м-у общим и конкретным состояниями будет запомнено в виде факта порождения.

Пример «Служащий»

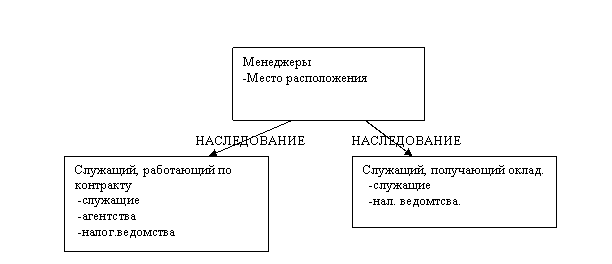
порождение(на_окладе,служащие).
порождение(по_контр,служащие).

%                   состояние  отдел
расположение_отдела(служащие,100,”корпус 1”).
расположение_отдела(служащие,200,”корпус 2”).
менеджер(служащие,100,”Маша”).
менеджер(служащие,200,”Коля”).
собрание(служащие,100,’вторник 14:00 Комната 125’).

%                      отдел оклад
служащие(на_окладе,Толя,100,200).
служащие(на_окладе,Вова,200,100).
налог_ведомость(на_окладе,2).
собрание_отдела(на_окладе,100,’Вторник 10:00 Комната 253’).

26. Математический нейрон Мак-Коллока-Питтса 

Исторически первой работой, заложившей теоретический фундамент для создания искусственных моделей нейронов и нейронных сетей, принято считать опубликованную в 1943 г. статью Уоррена С.Мак-каллока и Вальтера Питтса "Логическое исчислени идей, относящихся к нервной активности". Главный принцип теории Маккалока и Питтса заключается в том, что произвольные явления, относящиеся к высшей нервной деятельности, могут быть проанализированы и поняты, как некоторая активность в сети, состоящей из логических элементов, принимающих только два состояния ("все или ничего"). При этом для всякого логического выражения, удовлетворяющего указанным авторами условиям, может быть найдена сеть логических элементов, имеющая описываемое этим выражением поведение. Дискуссионные вопросы, касающиеся возможности моделирования психики, сознания и т.п. находятся за рамками этой книги.

Рис.4.1. Функциональная схема формального нейрона Маккалока и Пиитса.
В качестве модели такого логического элемента, получившего в дальнейшем название "формальный нейрон", была предложена схема, приведенная на Рис. 4.1. С современной точки зрения, формальный нейрон представляет собой математическую модель простого процессора, имеющего несколько входов и один выход. Вектор входных сигналов (поступающих через "дендриды") преобразуется нейроном в выходной сигнал (распространяющийся по "аксону") с использованием трех функциональных блоков: локальной памяти, блока суммирования и блока нелинейного преобразования.
Вектор локальной памяти содержит информацию о весовых множителях, с которыми входные сигналы будут интерпретироваться нейроном. Эти переменные веса являются аналогом чувствительности пластических синаптических контактов. Выбором весов достигается та или иная интегральная функция нейрона.
В блоке суммирования происходит накопление общего входного сигнала (обычно обозначаемого символом net), равного взвешенной сумме входов:

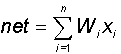
Выходной  сигнал нейрона
В модели Маккалока и Питтса отсутствуют временные задержки входных сигналов, поэтому значение net определяет полное внешненее возбуждение, воспринятое нейроном. Отклик нейрон далее описывается по принципу "все или ничего", т. е. переменная подвергается нелинейному пороговому преобразованию, при котором выход (состояние активации нейрона) Y устанавливается равным единице, если net > Q, и Y=0 в обратном случае. Значение порога Q (часто полагаемое равным нулю) также хранится в локальной памяти.
Фомальные нейроны могут быть объединены в сети путем замыкания выходов одних нейронов на входы других, и по мысли авторов модели, такая кибернетическая система с надлежаще выбранными весами может представлять произвольную логическую функцию. Для теоретического описания получаемых нейронных сетей предлагался математический язык исчисления логических предикатов.

27. Персептрон Розенблатта и правило Хебба

Персептрон Розенблатта является исторически первой обучаемой нейронной сетью. Существует несколько версий персептрона. Рассмотрим классический персептрон – сеть с пороговыми нейронами и входными сигналами, равными нулю или единице.

Определение персептрона

Персептрон должен решать задачу классификации на два класса по бинарным входным сигналам. Набор входных сигналов будем обозначать n-мерным вектором x. Все элементы вектора являются булевыми переменными (переменными принимающими значения «Истина» или «Ложь»). Однако иногда полезно оперировать числовыми значениями. Будем считать, что значению «ложь» соответствует числовое значение 0, а значению «Истина» соответствует 1.
Персептроном будем называть устройство, вычисляющее следующую функцию:
,
где  – веса персептрона, θ – порог,  – значения входных сигналов, скобки  означают переход от булевых (логических) значений к числовым значениям по правилам описанным выше. В качестве входных сигналов персептрона могут выступать как входные сигналы всей сети (переменные x), так и выходные значения других персептронов. Добавив постоянный единичный входной сигнал  и положив , персептрон можно переписать в следующем виде:

,

(1)

Очевидно, что выражение (1) вычисляется одним нейроном с пороговым нелинейным преобразователем (см. главу «Описание нейронных сетей»). Каскад из нескольких слоев таких нейронов называют многослойным персептроном. Далее в этой главе будут рассмотрены некоторые свойства персептронов. Детальное исследование персептронов приведено в работе [146].

Обучение персептрона. Правило Хебба

Персептрон обучают по правилу Хебба. Предъявляем на вход персептрона один пример. Если выходной сигнал персептрона совпадает с правильным ответом, то никаких действий предпринимать не надо. В случае ошибки необходимо обучить персептрон правильно решать данный пример. Ошибки могут быть двух типов. Рассмотрим каждый из них.
Первый тип ошибки – на выходе персептрона 0, а правильный ответ – 1. Для того, чтобы персептрон (1) выдавал правильный ответ необходимо, чтобы сумма в правой части (1) стала больше. Поскольку переменные  принимают значения 0 или 1, увеличение суммы может быть достигнуто за счет увеличения весов . Однако нет смысла увеличивать веса при переменных , которые равны нулю. Таким образом, следует увеличить веса  при тех переменных , которые равны 1. Для закрепления единичных сигналов с , следует провести туже процедуру и на всех остальных слоях.
Первое правило Хебба. Если на выходе персептрона получен 0, а правильный ответ равен 1, то необходимо увеличить веса связей между одновременно активными нейронами. При этом выходной персептрон считается активным. Входные сигналы считаются нейронами.
Второй тип ошибки – на выходе персептрона 1, а правильный ответ равен нулю. Для обучения правильному решению данного примера следует уменьшить сумму в правой части (1). Для этого необходимо уменьшить веса связей  при тех переменных , которые равны 1 (поскольку нет смысла уменьшать веса связей при равных нулю переменных ). Необходимо также провести эту процедуру для всех активных нейронов предыдущих слоев. В результате получаем второе правило Хебба.
Второе правило Хебба. Если на выходе персептрона получена 1, а правильный ответ равен 0, то необходимо уменьшить веса связей между одновременно активными нейронами.
Таким образом, процедура обучения сводится к последовательному перебору всех примеров обучающего множества с применением правил Хебба для обучения ошибочно решенных примеров. Если после очередного цикла предъявления всех примеров окажется, что все они решены правильно, то процедура обучения завершается.
Нерассмотренными осталось два вопроса. Первый – насколько надо увеличивать (уменьшать) веса связей при применении правила Хебба. Второй – о сходимости процедуры обучения. Ответы на первый из этих вопросов дан в следующем разделе. В работе [146] приведено доказательство следующих теорем:
Теорема о сходимости персептрона. Если существует вектор параметров α, при котором персептрон правильно решает все примеры обучающей выборки, то при обучении персептрона по правилу Хебба решение будет найдено за конечное число шагов.
Теорема о «зацикливании» персептрона. Если не существует вектора параметров α, при котором персептрон правильно решает все примеры обучающей выборки, то при обучении персептрона по правилу Хебба через конечное число шагов вектор весов начнет повторяться.
Доказательства этих теорем в данное учебное пособие не включены.

28. Алгоритм обучения персептрона

Алгоритм обучения персептрона
Персептрон обучают, подавая множество образов по одному на его вход и подстраивая веса до тех пор, пока для всех образов не будет достигнут требуемый выход. Допустим, что входные образы нанесены на демонстрационные карты. Каждая карта разбита на квадраты и от каждого квадрата на персептрон подается вход. Если в квадрате имеется линия, то от него подается единица, в противном случае - ноль. Множество квадратов на карте задает, таким образом, множество нулей и единиц, которое и подается на входы персептрона. Цель состоит в том, чтобы научить персептрон включать индикатор при подаче на него множества входов, задающих нечетное число, и не включать в случае четного.

Рис. 1.10. Персептронная система распознавания изображений
На рис. 2.10 показана такая персептронная конфигурация. Допустим, что вектор Х является образом распознаваемой демонстрационной карты. Каждая компонента (квадрат) Х - (x1, x2, :, xn) - умножается на соответствующую компоненту вектора весов W - (w1, w2, ..., wn). Эти произведения суммируются. Если сумма превышает порог Θ, то выход нейрона Y равен единице (индикатор зажигается), в противном случае он - ноль. Как мы видели в гл. 1, эта операция компактно записывается в векторной форме как Y = XW, а после нее следует пороговая операция.
Для обучения сети образ Х подается на вход и вычисляется выход Y. Если Y правилен, то ничего не меняется. Однако если выход неправилен, то веса, присоединенные к входам, усиливающим ошибочный результат, модифицируются, чтобы уменьшить ошибку.
Чтобы увидеть, как это осуществляется, допустим, что демонстрационная карта с цифрой 3 подана на вход и выход Y равен 1 (показывая нечетность). Так как это правильный ответ, то веса не изменяются. Если, однако, на вход подается карта с номером 4 и выход Y равен единице (нечетный), то веса, присоединенные к единичным входам, должны быть уменьшены, так как они стремятся дать неверный результат. Аналогично, если карта с номером 3 дает нулевой выход, то веса, присоединенные к единичным входам, должны быть увеличены, чтобы скорректировать ошибку.
Этот метод обучения может быть подытожен следующим образом:
1. Подать входной образ и вычислить Y.
2 а. Если выход правильный, то перейти на шаг 1;
б. Если выход неправильный и равен нулю, то добавить все входы к соответствующим им весам; или
в. Если выход неправильный и равен единице, то вычесть каждый вход из соответствующего ему веса.
3. Перейти на шаг 1.
За конечное число шагов сеть научится разделять карты на четные и нечетные при условии, что множество цифр линейно разделимо. Это значит, что для всех нечетных карт выход будет больше порога, а для всех четных - меньше. Отметим, что это обучение глобально, т. е. сеть обучается на всем множестве карт. Возникает вопрос о том, как это множество должно предъявляться, чтобы минимизировать время обучения. Должны ли элементы множества предъявляться- последовательно друг за другом или карты следует выбирать случайно? Несложная теория служит здесь путеводителем.

29. Дельта-правило и распознавание букв

Важное обобщение алгоритма обучения персептрона, называемое дельта-правилом, переносит этот метод на непрерывные входы и выходы. Чтобы понять, как оно было получено, шаг 2 алгоритма обучения персептрона может быть сформулирован в обобщенной форме с помощью введения величины δ, которая равна разности между требуемым или целевым выходом T и реальным выходом Y
δ = (T - Y). (2.3)
Случай, когда δ=0, соответствует шагу 2а, когда выход правилен и в сети ничего не изменяется. Шаг 2б соответствует случаю δ > 0, а шаг 2в случаю δ < 0.
В любом из этих случаев персептронный алгоритм обучения сохраняется, если δ умножается на величину каждого входа хi и это произведение добавляется к соответствующему весу. С целью обобщения вводится коэффициент <скорости обучения> η), который умножается на δхi, что позволяет управлять средней величиной изменения весов.
В алгебраической форме записи
Δi = ηδxi, (2.4)                                      w(n+1) = w(n) + Δi, (2.5)
где Δi - коррекция, связанная с i-м входом хi; wi(n+1) - значение веса i после коррекции; wi{n) -значение веса i до коррекции.
Дельта-правило модифицирует веса в соответствии с требуемым и действительным значениями выхода каждой полярности как для непрерывных, так и для бинарных входов и выходов. Эти свойства открыли множество новых приложений.

30. Обобщенное дельта-правило

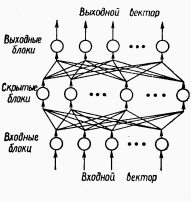Рассмотрим многослойную нейроподобную сеть с прямыми связями (см. рисунок). Входные элементы (блоки) образуют нижний слой сети, выходные - верхний. Между ними может быть много слоев скрытых блоков. Каждый блок может быть соединен модифицируемой связью с любым блоком соседних слоев, но между блоками одного слоя связей нет. Каждый блок может посылать выходной сигнал только р вышележащие слои и принимать входные сигналы только от нижележащих слоев. Входной вектор подается на нижний слой, а выходной вектор определяется путем поочередного вычисления уровней активности элементов каждого слоя (снизу - вверх) с использованием уже известных значений активности элементов предшествующих слоев. С точки зрения распознавания образов входной вектор соответствует набору признаков, а выходной - классу образов. Скрытый слой используется для представления области знаний.
Перед началом обучения связям присваиваются небольшие случайные значения. Каждая итерация процедуры состоит из двух фаз. Во время первой фазы на сеть подается входной вектор путем установки в нужное состояние входных элементов. Затем входные сигналы распространяются по сети, порождая некоторый выходной вектор. Для работы алгоритма требуется, чтобы характеристика вход-выход нейроподобных элементов была неубывающей и имела ограниченную производную. Обычно для этого используют сигмоидную нелинейность вида (4).
Полученный выходной вектор сравнивается с требуемым. Если они совпадают, обучение не происходит. В противном случае вычисляется разница между фактическими и требуемыми выходными значениями, которая передается последовательно от выходного слоя к входному. На основании этой информации об ошибке производится модификация связей в соответствии с обобщенным дельта правилом, которое имеет вид:
(6)
где изменение в силе связи wij для р-й обучающей пары пропорционально произведению сигнала ошибки д j-го блока, получающего входной сигнал по этой связи, и выходного сигнала блока i, посылающего сигнал по этой связи. Определение сигнала ошибки является рекурсивным процессом, который начинается с выходных блоков. Для выходного блока сигнал ошибки:
(7)
где djp и ojp - желаемое и действительное значения выходного сигнала j-го блока; уj' - производная нелинейности блока. Сигнал ошибки для скрытого блока определяется рекурсивно через сигнал ошибки блоков, с которым соединен его выход, и веса этих связей:
(8)

31. Активационные функции нейрона

Нужно отметить, что сегодня, спустя 50 лет после работы Маккалока и Питтса, исчерпывающей теории синтеза логических нейронных сетей с произвольной функцией, по-видимому, нет. Наиболее продвинутыми оказались исследования в области многослойных систем и сетей с симметричными связями. Большинство моделей опираются в своей основе на различных модификациях формального нейрона. Важным развитием теории формального нейрона является переход к аналоговым (непрерывным) сигналам, а также к различным типам нелинейных переходных функций. Опишем наиболее широко используемые типы переходных функций Y=f(net).
Пороговая функция (рассмотренная Маккалоком и Питтсом):

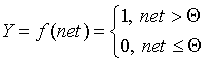
Линейная функция, а также ее вариант - линейная функция с погашением отрицательных сигналов:

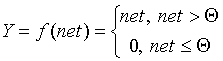
Сигмоидальная функция:

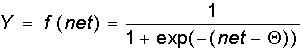
Как указывалось еще С.Гроссбергом, сигмоидальная функция обладает избирательной чувствительностью к сигналам разной интенсивности, что соответсвует биологическим данным. Наибольшая чувствительность наблюдается вблизи порога, где малые изменения сигнала net приводят к ощутимым изменениям выхода. Напротив, к вариациям сигнала в областях значительно выше или ниже порогового уровня сигмоидальная функция не чувствительна, так как ее производная при больших и малых аргументах стремится к нулю.
В последнее время также рассматриваются математические модели формальных нейронов, учитывающие нелинейные корреляции между входами. Для нейронов Маккалока и Питтса предложены электротехнические аналоги, позволяющие проводить прямое аппаратное моделирование.

32. Ограниченность однослойного персептрона

y=(x1 and Not x2) or (x2 and Not x1)

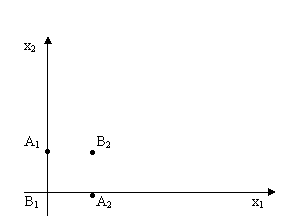
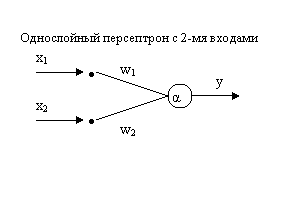
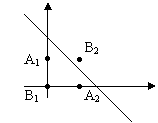
x1w1+ x2w2 = α – уравнение прямой. x1,x2 – переменные, w1,w2,α – постоянные.
Для всех точек выше линии x1w1+ x2w2 >α, тогда y=1.
                               ниже линии x1w1+ x2w2 <α, тогда y=0.

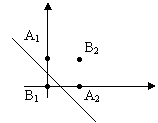
В A1,B2,A2 y=1.

Надо, чтобы A1 и A2 лежали под
прямой, а B1 и B2 – над прямой.

Однослойный персептрон не может решить эту задачу.

33. Многослойный персептрон

Рассмотрим иерархическую сетевую структуру, в которой связанные между собой нейроны (узлы сети) об'единены в несколько слоев (Рис. 6.1). На возможность построения таких архитектур указал еще Ф.Розенблатт, однако им не была решена проблема обучения. Межнейронные синаптические связи сети устроены таким образом, что каждый нейрон на данном уровне иерархии принимает и обрабатывает сигналы от каждого нейрона более низкого уровня. Таким образом, в данной сети имеется выделенное направление распостранения нейроимпульсов - от входного слоя через один (или несколько) скрытых слоев к выходному слою нейронов. Нейросеть такой топологии мы будем называть обобщенным многослойным персептроном или, если это не будет вызывать недоразумений, просто персептроном.

Рис.6.1. Структура многослойного персептрона с пятью входами, тремя нейронами в скрытом слое, и одним нейроном выходного слоя.
Персептрон представляет собой сеть, состоящую из нескольких последовательно соединенных слоев формальных нейронов МакКаллока и Питтса. На низшем уровне иерархии находится входной слой, состоящий из сенсорных элементов, задачей которого является только прием и распространение по сети входной информации. Далее имеются один или, реже, несколько скрытых слоев. Каждый нейрон на скрытом слое имеет несколько входов, соединенных с выходами нейронов предыдущего слоя или непосредственно со входными сенсорами X1..Xn, и один выход. Нейрон характеризуется уникальным вектором весовых коэффициентов w. Веса всех нейронов слоя формируют матрицу, которую мы будем обозначать V или W. Функция нейрона состоит в вычислении взвешенной суммы его входов с дальнейшим нелинейным преобразованием ее в выходной сигнал:
(6.1)
Выходы нейронов последнего, выходного, слоя описывают результат классификации Y=Y(X). Особенности работы персептрона состоят в следующем. Каждый нейрон суммирует поступающие к нему сигналы от нейронов предыдущего уровня иерархии с весами, определяемыми состояниями синапсов, и формирует ответный сигнал (переходит в возбужденное состояние), если полученная сумма выше порогового значения. Персептрон переводит входной образ, определяющий степени возбуждения нейронов самого нижнего уровня иерахии, в выходной образ, определяемый нейронами самого верхнего уровня. Число последних, обычно, сравнительно невелико. Состояние возбуждения нейрона на верхнем уровне говорит о принадлежности входного образа к той или иной категории.
Традиционно рассматривается аналоговая логика, при которой допустимые состояния синаптических связей определяются произвольными действительными числами, а степени активности нейронов - действительными числами между 0 и 1. Иногда исследуются также модели с дискретной арифметикой, в которой синапс характеризуется двумя булевыми переменными: активностью (0 или 1) и полярностью (-1 или +1), что соответствует трехзначной логике. Состояния нейронов могут при этом описываться одной булевой переменной. Данный дискретный подход делает конфигурационное пространство состояний нейронной сети конечным (не говоря уже о преимуществах при аппаратной реализации).

34. Алгоритм обратного распространения ошибки

позволяет определить коэффициенты w, α. Рассмотрим алгоритм для 2-хслойного персептрона.
N-входы
I-выходы

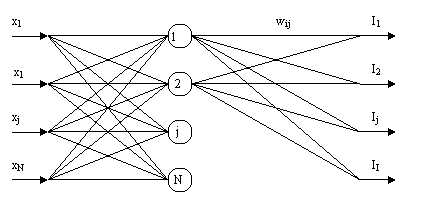
I-кол-во нейронов
wjN          j – номер нейрона в промежут. слое
                n – номер входа

Алгоритм обучения для выходного слоя
wij(t+1)=wij(t)+Δwij
Δwij = βεiyi, где εi=(di-yi)yi(1- yi),      di – выход слоя.

                                                               Алгоритм обучения для  промежуточного слоя
wjn(t+1)=wjn(t)+Δwjn
Δwjn = βεixn, где εj=(dj-yj)yj(1- yj),    dj – выход слоя неизв. dj заменяют. Ошибку на выходе dj выражают через di

dJ-yj=                 
Алгоритм обобщается на несколько слоев.
Внесем изменения: к сумме, к-ую выч. нейроне добавляется порог (смещение).
Si=
x0=1, всегда. wi0  - задается случайным образом.
Si= (x0=1).

Алгоритм обратного распространения ошибки для многослойного персептрона.

Пусть количество слоев K.
номер слоя h
колич. нейтронов в k-ом слое Hk.
i - порядковый номер нейрона в k-м слое
j – пор. номер нейрона в (k-1)-м слое
L – номер нейрона в (k+1)-м слое

Алгоритм

1. Инициализация синоптических весов и смещений

k=1..K
i=1..Hk
j=1..Hk-1
Синоптическим весам присваиваются малые случ. величины из интервала [-1,1].

2. Предстваление из обучающей выборки очередного вх-го вектора xq и соотв. вых век-ра Dq.

xq=(x1,x2,…,xn)q.
Dq=(d1,d2,…,dn)q.

3. Прямой проход

В циклах по k и i выч. выходные сигналы i-го нейрона в k-ом слое.

4. Обратный проход.

В циклах               k=K…1
                               i=1..Hk
                               j=1..Hk-1
выч веса

5. Выч. синоптические веса на новом шаге, где для вых слоя Δwij выч как для однослойного, а для пром. слоев используется алгоритм обратного распространения ошибки.

wij(k)(t+1)= wij(k)(t)+ Δwij(k)(t+1)    для k-го слоя.
Δwij(k)(t+1)  = βεi(k)yj(k-1), где
для вых слоя εi(k)=(di-yi) yi(1-yi)
для пром. слоев εi(k)= yi(k) (1-yi(k))

6. Повторение шагов 2-4 необходимое количество раз (сколько обучающих примеров).

Выч среднеквадратичн. ошибка ε=.
Q – кол-во обучающих примеров
М – кол-во слоев

Итерационный процесс заканчивается когда б. достигнуто заданное значение ε.

35. Задачи, решаемые с помощью нейросетей

Нейронные сети представляют собой новую и весьма перспективную вычислительную технологию, дающую новые подходы к исследованию динамических задач в экономической области. Первоначально нейронные сети открыли новые возможности в области распознавания образов, затем к этому прибавились статистические и основанные на методах искусственного интеллекта средства поддержки принятия решений и решения задач в сфере экономики.
Основная направленность – области, связанные с искусственным интеллектом.

Классификация.
Отметим, что задачи классификации (типа распознавания букв) очень плохо алгоритмизуются. Если в случае распознавания букв верный ответ очевиден для нас заранее, то в более сложных практических задачах обученная нейросеть выступает как эксперт, обладающий большим опытом и способный дать ответ на трудный вопрос.

Примером такой задачи служит медицинская диагностика, где сеть может учитывать большое количество числовых параметров (энцефалограмма, давление, вес и т.д.). Конечно, "мнение" сети в этом случае нельзя считать окончательным.
Классификация предприятий по степени их перспективности - это уже привычный способ использования нейросетей в практике западных компаний. При этом сеть также использует множество экономических показателей, сложным образом связанных между собой.

Нейросетевой подход особенно эффективен в задачах экспертной оценки по той причине, что он сочетает в себе способность компьютера к обработке чисел и способность мозга к обобщению и распознаванию. Говорят, что у хорошего врача способность к распознаванию в своей области столь велика, что он может провести приблизительную диагностику уже по внешнему виду пациента. Можно согласиться также, что опытный трейдер чувствует направление движения рынка по виду графика. Однако в первом случае все факторы наглядны, то есть характеристики пациента мгновенно воспринимаются мозгом как "бледное лицо", "блеск в глазах" и т.д. Во втором же случае учитывается только один фактор, показанный на графике - курс за определенный период времени. Нейросеть позволяет обрабатывать огромное количество факторов (до нескольких тысяч), независимо от их наглядности - это универсальный "хороший врач", который может поставить свой диагноз в любой области.
Прогнозирование.
Задачи прогнозирования особенно важны для практики, в частности, для финансовых приложений, поэтому поясним способы применения нейросетей в этой области более подробно.
Рассмотрим практическую задачу, ответ в которой неочевиден - задачу прогнозирования курса акций на 1 день вперед.
Пусть у нас имеется база данных, содержащая значения курса за последние 300 дней. Простейший вариант в данном случае - попытаться построить прогноз завтрашней цены на основе курсов за последние несколько дней. Понятно, что прогнозирующая сеть должна иметь всего один выход и столько входов, сколько предыдущих значений мы хотим использовать для прогноза - например, 4 последних значения. Составить обучающий пример очень просто - входными значениями будут курсы за 4 последовательных дня, а желаемым выходом - известный нам курс в следующий день за этими четырьмя.
Если нейросеть совместима с какой-либо системой обработки электронных таблиц (например, Excel), то подготовка обучающей выборки состоит из следующих операций:

1. Скопировать столбец данных значений котировок в 4 соседних столбца.
2. Сдвинуть второй столбец на 1 ячейку вверх, третий столбец - на 2 ячейки вверх и т.д.